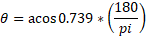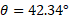Vector notation
A vector is a quantity in mathematics that has both magnitude and direction. An arrow pointing in a certain direction is a common way to depict a vector, with the length of the arrow denoting the magnitude of the vector.

Vectors are often written in boldface, underlined or with an arrow above the symbol.
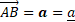
The purpose of doing this is to set them apart from scalars, which are objects that just have magnitude and no direction. For instance, a scalar quantity is a room's temperature, but a vector quantity is a moving object's velocity.
Column vectors
Column vectors are a way of writing the coordinates in which a vector is pointing towards. They can be written in 2D and 3D space.
A 2D column vector is a matrix consisting of a single column of numbers, with two elements. For example, the matrix:
is a 2D column vector. In this case, the vector could represent the coordinates (1, 2) in a two-dimensional coordinate system (x, y).
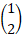
A 3D column vector is a matrix consisting of a single column of numbers, with three elements. For example, the matrix:
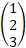
is a 3D column vector. In this case, the vector could represent the coordinates (1, 2, 3) in a three-dimensional coordinate system (x, y, z).
Component form
"i" and "j" are often used to represent the standard unit vectors in two-dimensional space. A unit vector is a vector with a magnitude of 1 that points in a specific direction.
The vector "i" is a unit vector that points in the positive x direction, and the vector "j" is a unit vector that points in the positive y direction.
For example:
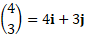
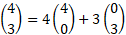
Magnitude and direction
The magnitude of a vector is simply the length based on two points.
Magnitude is denoted as the vector in modulus, which is the same as absolute value because the size can never be less than zero:
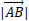
We can set a base of the vector being the x axis and the height from the base to the tallest or lowest point which is the y axis. Using Pythagoras’ theorem, we can determine the length as its simply calculating one side of a right-angled triangle:
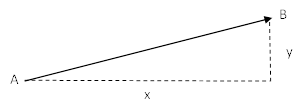
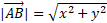
The direction of a vector is the angle in degrees from the x-axis. If two points are given then you can use both points to find the direction with respect to both, if only one point is given, then it can be determined that x and y are 0.
Direction is denoted by theta and you can use trigonometry to find the angle.
The formula to use would be tangent as we don’t have the hypotenuse:
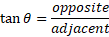
The opposite side is the difference in y values and the adjacent side is the difference in x values:
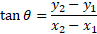
Therefore, the direction is simply the inverse tan of this. The result would be in radians which can by converted to degrees by multiplying the result by 180/pi:
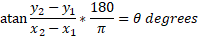
If given a magnitude and direction, then the vertical and horizontal components of the vector can be calculated using Pythagoras’ theorem as well.
The x component can be calculated using the following:
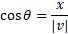
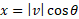
The y component can be calculated using the following:
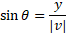
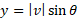
In both of these, the magnitude of the vector |v| is the hypotenuse.
Simplified then, the general formula for a vector with magnitude r and direction of theta can be written in component form as:
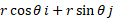
The direction should be calculated from the positive x axis and can go up to 360 degrees, so its important to note if the x or y is negative as this will impact on the direction and the angle can be obtuse.
Example
Calculate the magnitude and direction of the following vector:
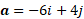
Answer:
To answer this question, you can first start with magnitude. The magnitude can be calculated using Pythagoras’ theorem:
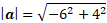
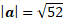
To answer the question on direction, it may be easier to draw a diagram first:
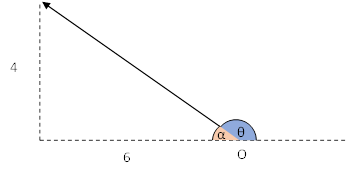
The length of the x component is always positive so the minus sign can be removed but it’s drawn in the negative x plane.
We need to find the angle theta as that is the direction of the vector from the origin.
We can calculate alpha first using Pythagoras’ theorem again and then subtract this from 180 as its on a straight line:
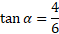
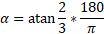
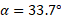
Subtract this from 180:
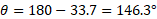
Written in final form, the vector is:
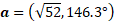
Angle between two vectors
When given two different vectors you can calculate the angle between them using trigonometry. Specifically using the cosine rule which will work with both 2D and 3D vectors.
So, using the formula:
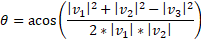
Where |v3| is the side opposite the angle.
Constructing a triangle to visually represent this information will make it easier to understand.
The angle can also be found using the dot product of vectors which results in a scaler that can be used in a formula to determine the angle.
The dot product vector rule is as follows:
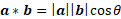
To rearrange this for solving for angle between vectors, you can solve for cosine theta and ultimately the inverse of this:
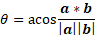
The dot product (a*b) can be calculated by multiplying each term in the vector by the other vector. This works for both 2D and 3D vectors:
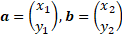
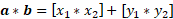
When substituting all these values into either formula and getting a result, the answer will be in radians and so this can be converted by multiplying the result by 180/pi.
Example using dot product
Find the angle between the vectors wa = 2i + j and b = 5i -3j
Answer:
We need to find the magnitudes of the vectors, the dot product of the vectors and substitute this into the formula for the angle:
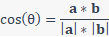


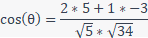
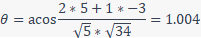
The angle needs to be converted to degrees from radians:
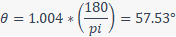
Example using cosine rule
Find the angle between the vectors a = -6i + 13j and b = i + 10j
To use the cosine rule we need to find the magnitude of the vector that connects the two vectors to form a triangle then substitute all the values into the cosine formula.
First find the magnitudes of all vectors:
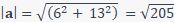

Calculate the connecting vector and its magnitude:
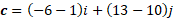
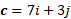
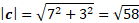
Now we can substitute into cosine formula:
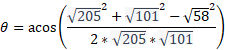
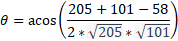
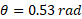
To convert this to degrees, multiply by 180/pi:
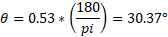
3D Vectors
3D Vectors operate in 3D space and have direction and magnitude like 2D vectors. The magnitude of a 3D vector can also be calculated using the Pythagorean theorem, and the angle between two 3D vectors can be calculated using the dot product or the cosine function, similar to 2D vectors.
A 3D column vector has 3 components:
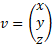
The letter used for the z value in component form is k, so the vector in component form is:
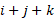
The magnitude of a 3D vector can be envisioned using a 3D space and calculating the sides already given and then finding the missing side for the vector itself:
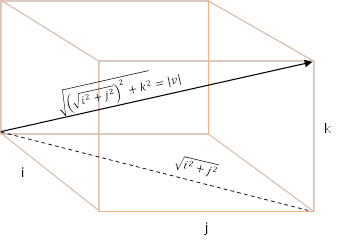
When given all 3 dimensions in vector form, they can correlate to the sides of 3D space such as in a cube like above. Then you can formulate triangles from the sides and use the same Pythagorean formula to calculate the missing sides of the triangle and ultimately the vector magnitude.
Example
Find the angle between the two 3D vectors below:
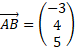
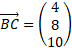
Answer:
Just like in 2D vectors you would find the magnitude of both of these vectors and then use this in a particular angle formula. For this one, we will use the dot product rule:
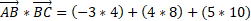
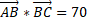
The magnitude of each vector can be calculated using the Pythagorean formula:
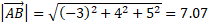
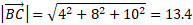
We can now substitute into the dot product formula for finding the angle:
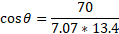
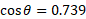
Solve for theta and convert to degrees: