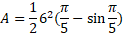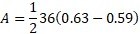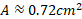Area of a triangle, sectors, segments and arc length

Area of a triangle

The area of a triangle can be calculated in a variety of ways depending on what attributes of the triangle are available to work with.

Insert area picture

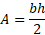
Area of an isosceles and scalene triangle:

Insert area picture

Derivation of the area of isosceles and scalene triangles:

These triangles can have an acute angle, obtuse angle and right-angle, all of which have the same result but have different methods in getting there.

A right triangle is the easiest to derive as if you reflect the same shape on the hypotenuse, you will get a rectangle. The area of a rectangle is base x height. So, half of this will give the right-angle triangle area:

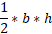
An acute angled triangle can be split into two right-angled triangles. Doing this splits the base into two separate values, in this case we can call them x and y.

So,

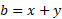
Substituting the base of each triangle into the original formula for the area of a triangle we get the following:

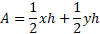
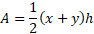
Hence,

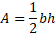
An obtuse angled triangle can have an additional right-angled triangle added onto the original to make a new whole right-angled triangle.

There is a new base which can now be split into two variables.

Substituting into the area equation and taking off the additional area we find the equation is still the same:

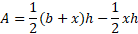
Expand the brackets:

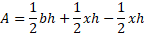
The final two terms cancel leaving the original formula:

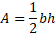
Area of an equilateral triangle:

Insert area triangle

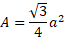
Derivation of the area of an equilateral triangle:

We can substitute the same values into the original formula using a as the base and the height being the altitude from the base to the peak:

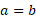
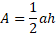
The height can be found using the Pythagorean theorem and splitting the triangle into two right-angled triangles.

The base would become half of a, c is simply a because sides are equal and so we can solve for h:

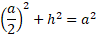
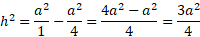
Square root every term for h:

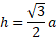
This can now be substituted back into the original formula:

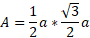
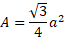
Area of any triangle with an angle between 2 given sides:

Insert area picture

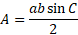
Derivation of the area of a triangle with included angle:

We can use trigonometric functions substituted into the original area of the triangle formula to derive this formula.

If we begin drawing an altitude, h, we can work out the length of the side if given the angle:

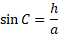
Solving for h:

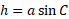
Substituting this into the original formula we get:

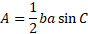
Rewritten gives the formula to begin with:

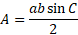
Area of any triangle given only sides and no height or angles using Heron’s formula:

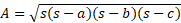
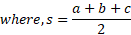
Derivation of Heron’s formula:

Heron’s formula uses the same formula for the area of a triangle in terms of only sides. You can work out the altitude (h) in terms of the all the other sides and then use algebra to simplify the expression.

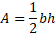
We can split the base into 2 parts:

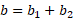
Using the Pythagorean theorem, we can express sides a and b with terms of h:

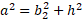
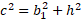
If we solve for either of the split bases in terms of just a b and c, we can use this to work out h in the same way.

We can start by taking away the equations from each other making the h cancel:

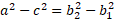
Knowing that both sides are the difference between two squares we can establish that one of the terms with both b’s will equal to the b term we established earlier which is:

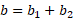
Now we can solve for any of the b’s, in this case we will solve for b₂:

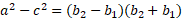
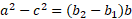
We can now divide through by b:

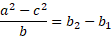
If:

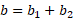
We can add the equations so solve for b₂:

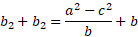
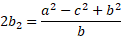
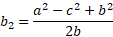
Now we have the value for one of the part bases in terms of all the known sides, we can now solve for h:

We have h in terms of part of a base already, which is b₂ from earlier:

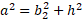
Rearranging for h only:

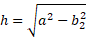
Substituting b2 into this equation provides h in terms of all the sides which is what we needed:

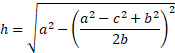
We can now substitute this back into the original area formula:

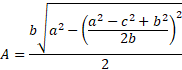
We can simplify this a lot to get to the original heron’s formula.

Firstly, we can remove the 2b from the top of the first fraction:

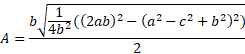
We can now put everything in one square root and use the difference of 2 squares:

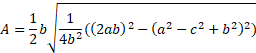
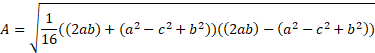
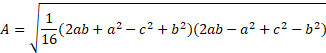
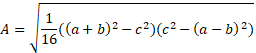
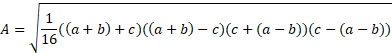
As there are 4 terms within the square root, we can divide the 1/16 through equally:

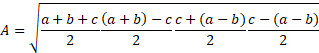
If we take the semi-perimeter to be S:

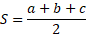
Then we can use that for the first term:

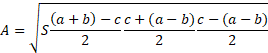
If we take the first term:

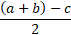
This is equal to the following:

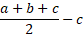
Hence:

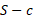
The remaining terms are same but for the different sides and we can rearrange for the original formula:

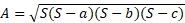
Sector, segments and arcs of a circle

Arc length

Insert arc length picture

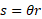
The arc length is a portion of the circumference of a circle. The formula is simple to define as it is simply the angle between the two radius lines multiplied by the radius. The arc length is usually denoted with an s.

Derivation of arc length:

If we use the fact that the circumference of a circle is the following:

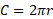
Part of this circumference would simply be the scale value in which the angle will describe how short it is.

Multiplying the circumference by the angle in radians over the circumference angle we get the following:

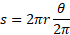
This cancels to give the circumference. But if we changed the angle to be half of the circle for example which is 2pi/2 which is just pi we get the following:

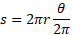
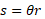
This can continue for any angle and satisfies the original statement.

Example

Calculate the following distance of the curve AB for the diagram below:

We are given the angle which is in radians and the two sides which would be the radius of the circle as they are both equal. Simply substitute into the formula:

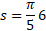
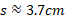
Sector area

Insert sector picture

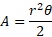
The area of a sector is just a portion of the area of a whole circle. The angle is used in the formula as a scale factor to how big the sector is compared to the whole circle.

Derivation of the sector area:

Given the area of a circle to be:

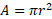
Then we can use this as the base area and simply times it by the scale factor of what the sector is, which is defined by the angle itself.

The angle scale factor is the angle given divided by the entire angle of the circle:

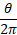
So:

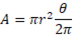
This can cancel to the original formula:

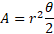
Example

Calculate the area of the given sector in the diagram below:

The angle and radius are provided so we can simply substitute the values into the formula:

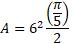
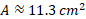
Segment area

Insert segment picture

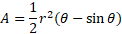
The area of a segment when inspected closely is simply the area of a sector minus the area of the triangle formed within that sector. The segment area uses the same angle properties to determine the difference of areas.

Derivation of the segment area;

Given the sector area to be:

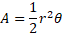
And the triangle area to be:

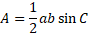
The difference between them provides the segment area:

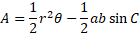
Given that a and b in the triangle portion/second term of this equation is the radius and C is the angle between the radius which is the common angle theta, we can substitute these values:

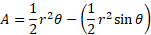
Simplifying gives the original formula:

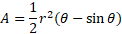
Example

Calculate the shaded area of the diagram below:

We are given the angle and radius here so we can substitute the values into the equation for segment area: