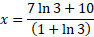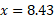Notation, terminology and laws
Logarithms are mathematical operations that calculate the exponent that a base number must be raised to in order to obtain a given number.
Logarithms and exponents are related because a logarithm can be used to find the exponent of a number, and an exponent can be used to find the logarithm of a number.
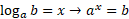
A logarithm needs a base number, in the case above that is the variable ‘a’. The base number is the number in which you are raising powers to.
The laws for working with logarithms are the inverse of the laws of exponents. They are as follows:
Adding logs:
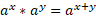
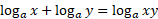
Subtracting logs:
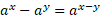
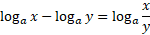
Logs raised to powers:
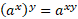
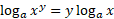
Same base logs:
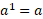
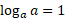
Log of 1:
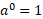
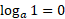
Example (simple)
- Simplify the following logarithm:
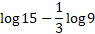
Answer:
Simplifying a logarithm means to put the log in its smallest form, this can be done by combining the logs using the logs laws:
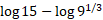
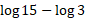
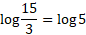
Example (advanced)
- Solve the below equation for variable x, where x > 1:
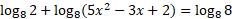
Answer:
The equation uses a variety of log laws as well as additional algebra such as quadratic equations to solve for x. First step is to combine the logs as they have the same base:
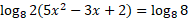
The logs cancel by using 8 raised to the power of both sides leaving the following quadratic:
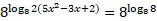
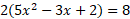
Simplifying the quadratic:
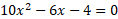
Using quadratic formula to get the values of x:
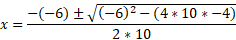
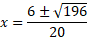
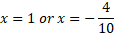
Since x is positive, the answer has to be x = 1.
Natural Logs (ln)
Natural logarithms are logarithms with base e, commonly referred to as logarithms to the base e. (2.71828). They are mostly utilised in calculus and are implemented in exponential growth and decay questions. Natural logarithms are more beneficial for exponential growth and decay problems as well calculus applications than conventional logarithms, which are logarithms to the base 10.
Natural logs being just the normal logs with a base of Euler‘s number but rewritten in natural log form:
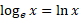
The natural log and e are inverses of each other so the following statements would cancel and give you x on its own:
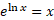
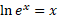
Natural logs can be used in the same way as logs to work out exponential equations:
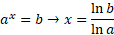
This is derived using the normal log laws:
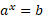
Take natural log of both sides:
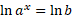
Using exponential log laws, the x can be brought to the front:
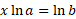
Dividing both sides by the natural log of a gives x:
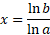
Example (simple)
- Solve the below equation for variable x to 3 significant figures:
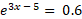
Answer:
As the equation uses e, we can take the natural logarithm of both sides. The natural log of e to an exponent simply leaves the exponent on its own:
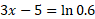
Then rearrange for x:
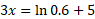
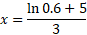
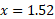
Example (Advanced)
- Solve the below equation for variable x to 3 significant figures:
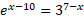
Answer:
First step is to take the natural logarithm of both sides in order to get x out of exponent:
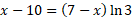
Expand the right side:
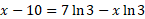
Get all variables to one side:
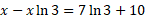
Factorise the left side:
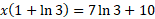
Solve for x: