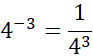Laws of exponents
There are a few laws of exponents that are very important to understand in order to functionally apply to most mathematical equations.
Exponents may be called powers or indices and mean the same thing.
First rule for multiplying indices:
Simply add the powers together when the base number is the same
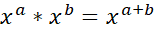
E.g.
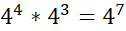
Second rule for dividing indices:
Subtract the powers when dividing with the same base number
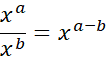
E.g.
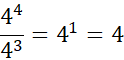
Third rule for raising indices to another power:
A power raised to a power such as when in parenthesis, you can simply multiple the powers together
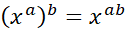
E.g.
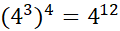
Forth rule for any number raised to power of zero:
Any base number raised to the power of 0 always equals 1
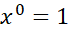
E.g.
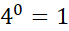
Fifth rule for interpreting fractional powers with 1 as numerator as roots:
Numbers raised to a fraction means a root is involved, when its 1 then the denominator determines the root power.
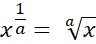
E.g.
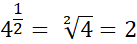
Sixth rule for varying fractal powers:
Numbers with a numerator larger than 1, the numerator becomes the power raised to the base and then the root power is the denominator.
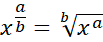
E.g.
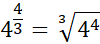
Final rule for negative indices:
Negative powers mean the result is a fraction and the base is still raised to the initial power but its now positive.
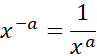
E.g.