Properties of linear function graphs
Linear equations are the simplest of equations to graph. When you see the terms linear, it means practically means constant rate and so you can imagine this graph as a straight-line graph.
There are some terms that one should know when graphing equations:
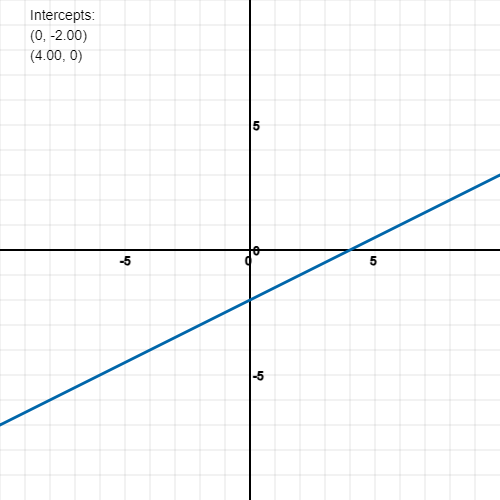
Y-intercept: This is related to when the line on the graph crosses a point where the X component is 0, the Y value at this point is the Y-intercept.
X-intercept: This is related to when the line on the graph crosses a point where the Y component is 0, the X value at this point is the X-intercept.
Slope/gradient: This calculated using something called rise over run. If you pick a point on the line and then another point on that same line, you can count how much you need to go up the Y component (rise) and how much you need to go across the X component (run) to meet that point. You divide these numbers for the gradient.
Slope can be written as the formula:
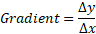
Linear equations can be identified by the fact they won’t have exponents in the equation. They can also be identified based on the format they are written in.
There are 3 types of linear equations:
- Point slope form
- Slope intercept form
- Standard form
Formula of Point slope form:
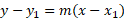
Point slope is used to determine a single point and the slope of a line. The m term in the equation relates to the slope.
Formula for Slope intercept form:
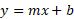
Slope intercept is used to determine the slope and y intercept of a line. The b term in the equation relates to the y intercept value (0, b). The m term in the equation relates to the slope.
Formula for standard form:
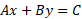
Standard form is used to solve equations in this form and A cannot be a negative number. A, B and C are whole numbers.
The equations above are often interchangeable and you can work out specific things when you have solved one. For example, point slope form can be converted to slope intercept form for the y-intercept.
Examples:
- Given two points: (2, 3) and (-3, 1), work out the gradient of the line.
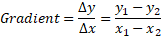
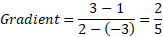
It doesn’t matter how we substitute, if we made y2 = 3 and x2 = 2, the answer will still be the same as the negative signs in both the numerator and denominator would cancel.
This makes sense logically if you imagine a line with two points, you can select either point and the slope is still going to be the same angle on the graph.
- Given one point: (-3,4) and a slope of 3, work out an equation for the y-intercept.
We can use the point slope form to work out an equation for the y-intercept when given one point and the slope. We just substitute the numbers.
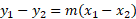
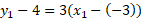
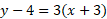
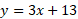
If you refer back to the notes above in the y-intercept form, you will see this matches that exact equation, hence these equations being related:
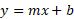
If we make x = 0 in this equation, it will give us the exact y-intercept for this line
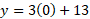
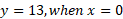
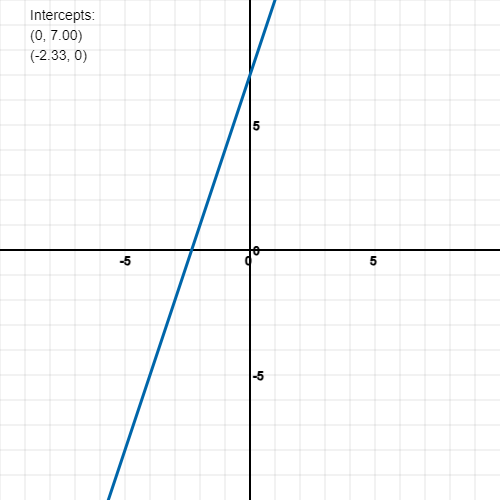
- Graph the equation y = 3x + 7
This equation is in the form y = mx + b and so we know that the slope is going to be 3 (m) and the y intercept will be 7.
The slope is 3/1 and so that means you can go 3 units up the y axis and 1 unit across to get to the next point. So doing this will present the following graph:
- Graph the equation 2x – 4y = 8
This equation is in the form of Ax + By = C and so we can start by finding by finding each intercept by making either the x value or y value 0 for each intercept.
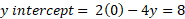
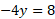
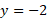
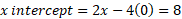
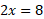
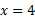
Now we have the values for both intercepts, we can draw the line connecting these points: