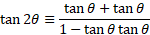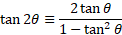Fundamental Trigonometry

Right-angled triangles

Right angled triangles have at least one 90-degree angle and the formulas used to calculate missing angles or sides in these triangles are specific to right-angled triangles only.

There are 3 formulas for working with sides and angles in these triangles:

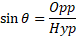
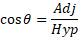
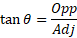
This is often abbreviated to SOH CAH TOA.

The sides of a triangle include the opposite, adjacent and the hypotenuse:

• Opposite side is the side of the triangle which is opposite the angle given.
• Adjacent side is the side next to the angle given.
• Hypotenuse is the side opposite the right angle.

Theta (Θ) represents the angle between the sides of the triangle. This can be given or missing to work out sides or angles depending on the question at hand.

You can inverse all of these trigonometric functions to find actual angle values. The inverse of each trigonometric function is the following:

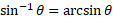
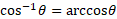
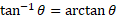
Another rule for working with right angled triangles is the Pythagorean theorem:

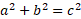
This rule dictates that the hypotenuse of a triangle (c) is equal to the sum of the other sides squared.

To solve a question relating to triangle geometry, you can follow the steps below:

1. Identify the type of triangle, if it is a right-angled triangle or not. Or if the triangle could be split into right-angled triangles and if that would be helpful.
2. Identify which sides are present and which are missing out of the hypotenuse, adjacent and opposite.
3. Identify which angles are given and which should be used to solve the question. In right-angled triangles there will always be a 90-degree angle but this is not used in the formulas.
4. Input the values into the correct formula and rearrange to solve for the missing variable.

Examples

These rules are best represented with examples so here are some examples of finding the sides and angles of right-angled triangles:

1. Find the missing angle theta in radians for the below triangle:

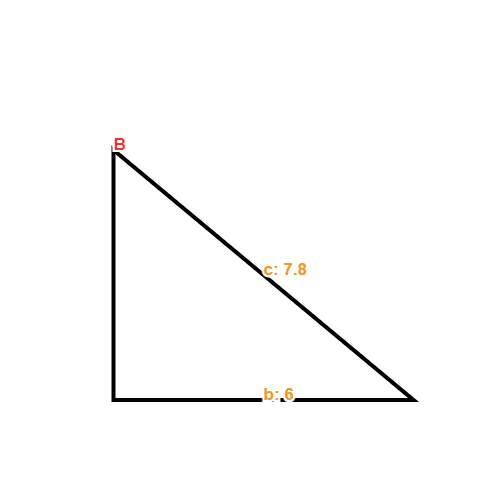
Firstly, we can identify the sides relative to the angle.

Hypotenuse = side c as it is opposite the right angle and we know the value to be 7.81.

Opposite side = side b as it is opposite the missing angle, and we know the value to be 6.

Adjacent side = side a as it is next to the angle. The value is not given.

So, we have the opposite side and the hypotenuse, the relevant formula for dealing with both of these sides is SOH:

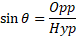
We can now substitute:

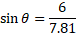
Using the inverse of the sin function we can get the value of theta:

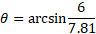
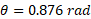
2. Find the value for side c for the below right-angled triangle:

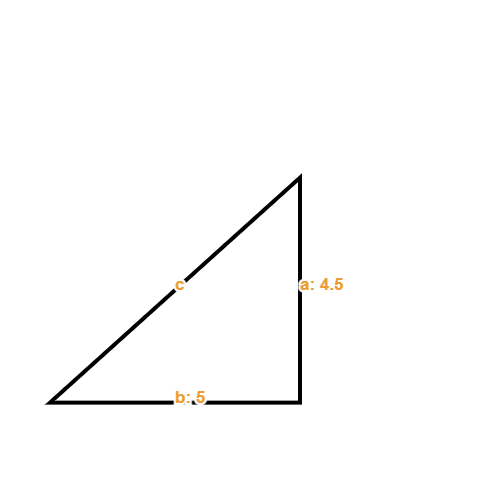
This question has one missing side so we can use the Pythagorean theorem to work out the missing side:

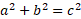
The missing side is the hypotenuse so we do not have to rearrange the equation to solve for a different side as c is the hypotenuse.

We can simply substitute:

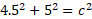
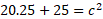
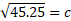
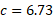
3. Find the value for side b for the below triangle:

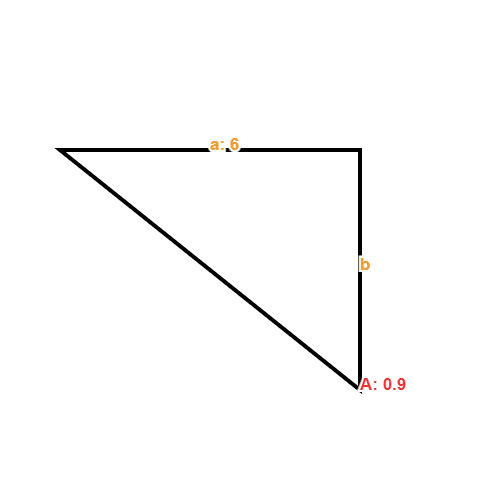
There is only one side given in this question so it rules out the ability to use the Pythagorean theorem as that would leave 2 missing variables and we need to solve for one.

We have an angle given in the triangle as well as one side. The side given is the opposite side as it is opposite the given angle.

The side to work out is the adjacent side as it is next to the angle.

The trigonometric formula for dealing with Adjacent sides is TOA:

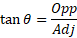
We don’t have the opposite side but we do have the angle. We can substitute and rearrange:

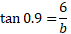
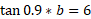
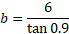
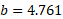
Unit circle

The term unit circle simply means a circle with radius 1 of any unit.

The visual representation of the unit circle can help to understand the units of radians and how a triangle can have radians specified in terms of pi radians.

Insert picture

If we draw a right-angled triangle in this circle, we can establish that it has 2 unknown point on the circle that have individual x and y values.

We know however that this is a unit circle and the radius is 1, so the hypotenuse of this triangle is 1. We also have the angle, so to work out the first point we know that the length of the adjacent side is going to also be the x value.

Using trigonometric functions, we know that cosine of the angle is the adjacent divided by the hypotenuse:

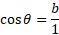
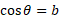
So, if b is the length and also the x value, we can equate the following:

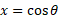
We can do the same for the y value. Since the y value will be the length of the opposite side, a, then we know that we just need to use trigonometric functions relevant to it. In this case it is sine of the angle equal to the opposite side over hypotenuse:

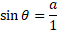
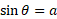
So, if a is the length and also the y value, we can equate the following:

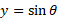
This is important because it now expands the values of sine and cosine outside of triangles and within a circle instead, allowing angles of more than 180 degrees or pi.

Using this we can also establish how radians work.

Radians are not a unit of measure but rather a ratio between the arc length and the radius of the circle. Knowing that the arc length of the entire circle is going to be 2*pi*r and this being the unit circle r is just 1, then arc length is just 2pi.

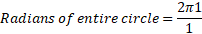
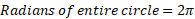
With this we can also work out other angles such as half a circle:

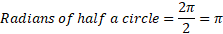
Insert image

This can continue for any angle you like and all the angles in radians are in terms of pi based on this unit circle. The radius of the circle does not affect the angle as all circles are the same shape. This gives a universal measure of how radians can be used to describe angles of any kind.

Sine rule

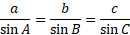
You can calculate sides and angles of any triangle if you are given specific angles and sides using the sine rule. This is regardless of if the triangle is a right-angled triangle or not.

If you are given a side and the angle opposite as well as another side or angle with its opposing side or angle missing, you can use the sine rule to calculate this.

Remember that the side opposite has the angle name relevant to that side name. For example, side a will always have angle A opposite. The same is for the others.

Derivation of the sine rule:

We can use the trigonometric equations to prove the sine rule by splitting any triangle into 2 right-angled triangles by the altitude (h) and introducing a new point X:

Using the following trigonometric equation for both triangles we get the following substitution:

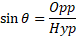
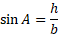
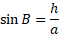
So, we can solve for h using all these variables:

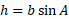
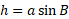
Therefore:

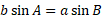
We can then rearrange the equation for opposite sides and angles being together:

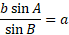
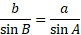
The same applies for angle C and side if you change the altitude to incorporate the angle as well with the same methods above, thus giving:

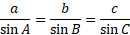
Examples

1. Find the value for side length a in the below triangle:

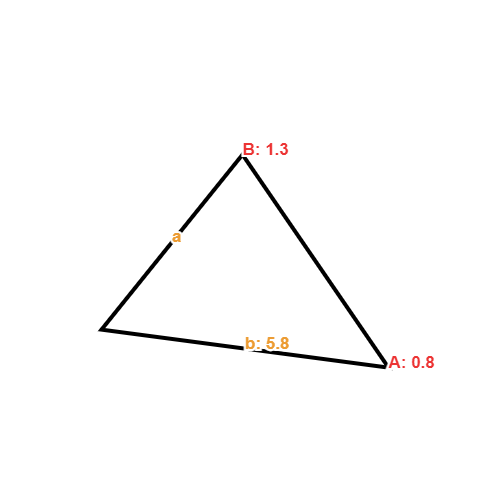
Firstly, we can identify what rule to use based on the missing sides and given sides/angles. In this example, we have side b, angle B and angle A. So, we can use the sine rule to workout side a:

2. Find the value for angle C in the below triangle:

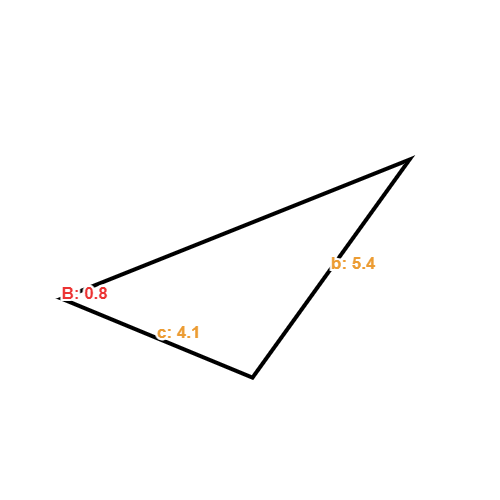
Identifying the sides and angles given, we can see that we have side c which is opposite the angle and we also have side b with its corresponding angle B.

Using this information, we can substitute the values:

Cosine rule

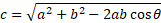
Rewriting this equation can give you the angle:

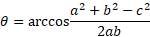
These equations can help find an angle when given all its sides and an opposite side when given 2 sides and an included angle.

The angle being worked out in the formula about is the angle between sides a and b, this however can be rearranged to find a different included angle if named differently.

Derivation of the cosine rule:

Using the trigonometric equations, we can define how cosine can help so solve sides and angles of triangles.

We can then split any triangle using the altitude of the triangle (h):

Side a is then split into 2 lengths:

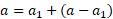
If we take substitute into Pythagoras’ theorem, we can find side h:

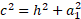
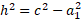
We can also find side b using the same method:

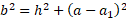
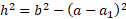
Thus:

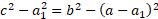
Expanding the brackets gives:

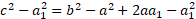
Simplifying:

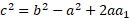
Now we can find a1 in terms of angles and sides using the relevant trigonometric equation:

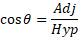
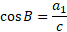
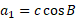
Substituting backing to the equation:

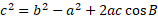
This can be rearranged to solve for a different angle:

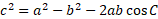
This is the original cosine rule.

Examples:

1. Find the missing angle in the below triangle:

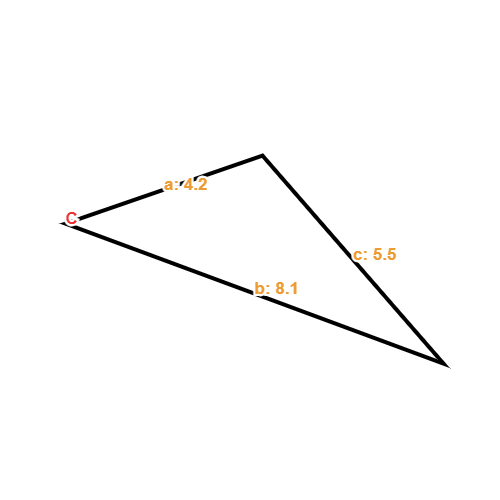
We have been given the sides between a missing angle and all sides are given. So, we know we can use the cosine rule to work out the missing angle.

The formula requires just the sides to work out this angle. Side c in the formula would be the side opposite the missing angle so now we can substitute knowing these facts:

2. Find the missing side in the below triangle:

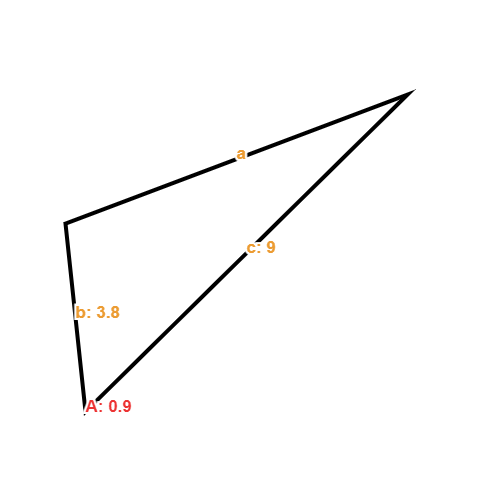
In this triangle with have values for side b and c but not a, however this does not change the equation. Because the sides and angles do not correlate with the equation. Angle A is between sides b and c and so we can use the equation as normal to solve for side a:

Trigonometric identities

Trigonometric identities equate different Pythagorean equations where they are true for any value, which make it an identity. They help break down different trigonometric functions into known functions.

The fundamental identities to know are the following:

Reciprocals:

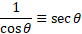
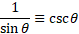
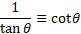
Ratios:

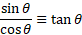
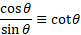
Compliments:

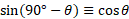
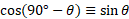
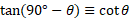
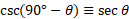
Pythagorean identity

Given the equation for a circle is the following:

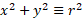
The unit circle has the radius 1 and we know that x and y can be substituted with trigonometric functions instead giving the following formula:

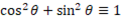
This is useful because it can now use the previous rules and convert to many useful identities:

If we rearrange, we get the following:

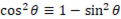
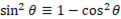
If we divide through by cos theta we get:

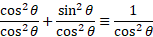
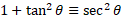
If we divide through by sin theta we get:

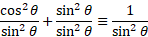
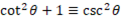
Compound angle identities:

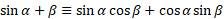
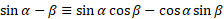
Using the above formulas, we can work out the same compound angle formula for cosine and tangent.

Using the compliment identity, we can work out terms in sine:

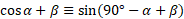
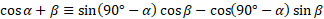
Simplified using compliments:

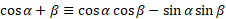
The signs can be switch to give the following:

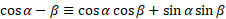
For tan, given we have an identity that links sine and cosine with tan we can rewrite the formula in these terms:

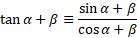
The terms we have now directly relate to the identities we established above and so we can substitute and work with that:

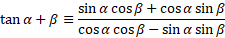
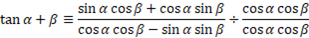
Using the tan ratio identity, it provides the following:

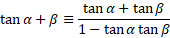
You can inverse the signs for the following:

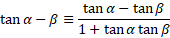
Double angle identities:

Using the above compound angle identities, we can let alpha and beta be the same giving 2x of the angle.

For sine double angle identity:

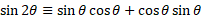
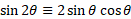
For cosine, there are multiple that can be derived using multiple identity rules:

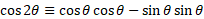
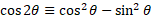
Given that:

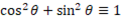
We can rearrange for sine and cosine:

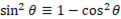
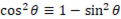
We can substitute these into the formula we derived for 2 other solutions in terms of cosine and sine only:

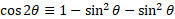
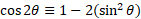
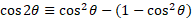
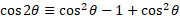
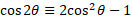
For tangent double angle identity: