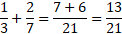Terms of a fraction
There are two terms when it comes to fractions. One is the denominator and the other is the numerator.
The numerator is the top number of a fraction and the denominator is the bottom part of the fraction.
Multiplying fractions
Multiplying fractions is probably the easiest operation when it comes to working with fractions.
There are two things to consider, which is simply are you multiplying a fraction against a whole number or multiplying a fraction with another fraction. Below are the formulas for both.
The first being for multiplying against a whole number:
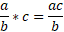
Second, multiplying two fractions together:
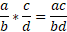
Example:
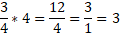
Example:
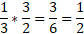
Simplifying a fraction, like what is done above, means that the two numbers in the fraction are common factors such as 3 and 6. You can determine how many times the numerator goes into itself and how many times the numerator goes into the denominator to find the simplest form of the fraction. The result doesn’t change.
Dividing fractions
Dividing fractions will use methods from multiplication except with a couple additional steps.
We can use something called the keep, change, flip method. You keep the first fraction the same. Change the sign from divide to multiply. Flip the numerator and denominator of the second fraction. After that, it’s a simple multiply method.
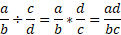
When it comes to dividing fractions by whole numbers. You can simply think of the whole number as being a fraction over 1. Because 1 goes into the whole number as many times as itself.
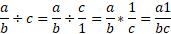
Example:
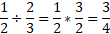
Example:
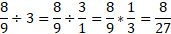
Subtracting fractions
Subtracting fractions is a little more complicated than other operations. This is because subtraction and addition are quite opposite to division and multiplication.
Subtracting and addition is practically the same operation except you change the signs relative to if its subtraction or addition.
When it comes to subtracting whole numbers from fractions, you need to multiply the denominator and the whole number and take it away from the numerator. Then you put that result over the original denominator:
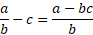
As for subtracting other fractions from a fraction, it’s a similar process except you multiply the first numerator with the second denominator and the first denominator with the second numerator. You can think of it like an X pattern when multiplying.
You subtract the first result from the second result and put that over the denominators multiplied together.
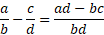
Example:
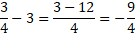
If either the numerator or denominator become negative numbers, you can make the whole fraction negative by putting the sign before the fraction. You can leave it either at the top or bottom and it will still mean the same, but just for clarity.
Example:
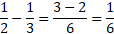
Adding fractions
Adding fractions is just like subtraction with the signs changed to addition.
When it comes to Adding whole numbers to other fractions, you need to multiply the denominator and the whole number and add it to the numerator. Then you put that result over the original denominator.
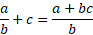
When adding fractions to other fractions, just like subtraction, you multiply the numerator with the second denominator and the first denominator with the second numerator.
Add the results together and divide over the denominators multiplied together.
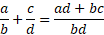
Example:
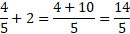
Example: