Binary Search Trees

A binary search tree (BST) is a data structure that stores elements in a hierarchical manner. Each node in the tree has at most two children, a left child and a right child. BSTs have the following properties:

1. The value of the left child is less than the value of its parent.
2. The value of the right child is greater than or equal to the value of its parent.
3. Both the left and right subtrees must also be binary search trees.

These properties ensure that BSTs have an ordered structure, which allows for efficient searching, insertion, and deletion operations.

Searching in a Binary Search Tree

To search for an element in a BST, start at the root node and follow the tree structure based on the element's value:

1. If the element is equal to the value of the current node, the search is successful.
2. If the element is less than the value of the current node, move to the left child.
3. If the element is greater than the value of the current node, move to the right child.
4. Repeat steps 1-3 until the element is found or there are no more nodes to traverse.

The time complexity of searching in a BST is O(h), where h is the height of the tree. In the best case, the tree is balanced, and the height is O(log n), where n is the number of nodes. In the worst case, the tree is completely unbalanced, and the height is O(n).

Insertion in a Binary Search Tree

To insert a new element into a BST, follow these steps:

1. Start at the root node.
2. If the new element is less than the value of the current node, move to the left child. If the left child is null, insert the new element as the left child.
3. If the new element is greater than or equal to the value of the current node, move to the right child. If the right child is null, insert the new element as the right child.
4. Repeat steps 2-3 until the new element is inserted.

The time complexity of insertion in a BST is also O(h), with best and worst cases similar to searching.

Deletion in a Binary Search Tree

To delete an element from a BST, follow these steps:

1. Search for the element in the BST.
2. If the element is found, determine which of the following cases applies:
   1. The node has no children: Simply remove the node.
   2. The node has one child: Replace the node with its child.
   3. The node has two children: Find the in-order predecessor (the maximum value in the left subtree) or the in-order successor (the minimum value in the right subtree), replace the node with the predecessor or successor, and delete the predecessor or successor.

The time complexity of deletion in a BST is O(h), with best and worst cases similar to searching and insertion.

Balancing a Binary Search Tree

To ensure that a BST maintains its efficiency, it is essential to keep the tree balanced. There are several techniques for balancing BSTs, including the following:

1. AVL Trees: AVL trees are a type of self-balancing binary search tree that maintains a balance factor for each node, ensuring that the height difference between the left and right subtrees is at most 1.
2. Red-Black Trees: Red-black trees are another type of self-balancing binary search tree that uses a colour property for each node to ensure that the tree remains approximately balanced.

Both AVL trees and red-black trees guarantee that the height of the tree is O(log n), ensuring optimal performance for searching, insertion, and deletion operations.

Traversal of a Binary Search Tree

Traversing a BST involves visiting each node in a specific order. There are three common types of tree traversal:

1. In-order traversal: Visit the left subtree, the current node, and then the right subtree. This traversal method results in the elements being visited in ascending order.
2. Pre-order traversal: Visit the current node, the left subtree, and then the right subtree. This traversal method is useful for creating a copy of the tree or for serialization.
3. Post-order traversal: Visit the left subtree, the right subtree, and then the current node. This traversal method is useful for deleting nodes or evaluating expressions in a tree structure.

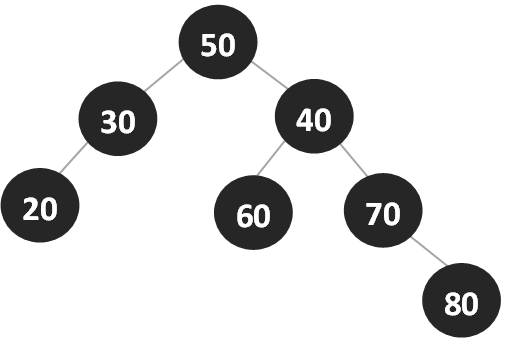
Example

Consider the following binary search tree from the start:

1. In-order traversal: 20, 30, 40, 50, 60, 70, 80
2. Pre-order traversal: 50, 30, 20, 40, 70, 60, 80
3. Post-order traversal: 20, 40, 30, 60, 80, 70, 50

Applications of Binary Search Trees

Binary search trees have various applications in computer science, including:

1. Symbol tables: BSTs can be used to implement symbol tables in compilers and interpreters for programming languages.
2. Databases: Database management systems use tree-based data structures like B-trees, which are generalizations of binary search trees, for efficient storage and retrieval of data.
3. Game AI: BSTs can be used to model game states and search for optimal moves in game artificial intelligence.

Exmaple Binary Search Tree in JavaScript